Een klein rekenexperiment is noodzakelijk, om te beginnen. Volg je mij even?
Stel je voor: in een kamer staat een emmer met daarin tien balletjes, negen blauwe en een rode. Een geblinddoekt persoon haalt een balletje uit de emmer zonder dat hij kan zien welke. Dan is de kans dat hij het rode balletje pakt dus tien procent of 0,1.. en de kans dat hij een van de negen blauwe balletjes pakt 90 procent of 0,9.. dat is niet zo moeilijk, toch?
Maar als we dit experiment tien maal herhalen, hoe groot is dan de kans dat de geblinddoekte persoon in een (of meer) van de gevallen het rode balletje pakt?
Dus: de geblinddoekte proefpersoon mag een balletje trekken, en als hij dat heeft gedaan doen we het balletje weer terug en mag hij het nog een keer doen, en dat dan tien keer.
Dat is een wat ingewikkelder som; ik wil niet verantwoordelijk zijn voor het met geweld openrijten van allerlei middelbare schoolcomplexen, maar toch even, de bijbehorende som heet ‘binomiale verdeling’ en klinkt als volgt:
P(X = k) =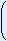 
n
k
k
k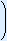
· pk · (1 – p)(n – k)
De invulling van deze som zal ik U besparen, het is ook niet heel belangrijk.
Met deze som kun je de kans berekenen dat precies een van de tien balletjes rood is als we het experiment tien maal herhalen, maar we willen weten hoe groot de kans is dat een of meer van de gekozen balletjes rood zijn. Dat vereist nog een extra som, die zal ik U ook besparen. Het komt er op neer dat de kans dat een of meer rode balletjes worden getrokken als we het emmer-experiment tien maar herhalen 0,65 of 65 procent is.
Goed, 65 procent. Dat onthouden we even.
Stel: je bent gevaccineerd, en de beschermingsgraad is 90 procent, dus je hebt 0,1 of tien procent kans besmet te raken wanneer je iemand tegenkomt die COVID-19 heeft en besmettelijk is. Die vaccinatie geeft je zelfvertrouwen en moed om je oude leven weer op te pakken, je knuffelt en feest en maakt een mooie inhaalslag, en stel dan dat je in de loop van een aantal weken of maanden tien mensen tegenkomt die COVID-19 onder de leden hebben en besmettelijk zijn. Dan is de kans dat jij ook besmet raakt dus 0,65 of 65 procent, net als bij het experiment met de blauwe en rode balletjes. Ondanks dat je gevaccineerd bent, ben je dus bepaald nog niet veilig voor besmetting.
Wij kunnen van dit alles twee dingen leren:
Ten eerste: als je gevaccineerd bent maar anderen nog niet, is het dus niet verstandig je oude levenspatroon weer op te pakken, elke dag diverse willekeurige mensen omhelzen en zo, omdat de vaccinatie geen cumulatieve bescherming biedt. De anderhalve meter en de handen wassen en zo zijn nog steeds geen overbodige maatregelen.
Ten tweede: groepsimmuniteit is heel belangrijk, hoe meer mensen gevaccineerd zijn, hoe voordeliger de verhouding rode/blauwe balletjes in de emmer, hoe kleiner de kans dat je besmet raakt. Als een bepaalde grens is bereikt (die kun je ook berekenen maar dat zou weer een enge som opleveren) kun je in principe weer gaan knuffelen wie je wilt. Dan is de kans dat je besmet raakt zo klein, dat het besmettingsreproductiegetal (ver) onder nul blijft.
Zo. Dat is de gedachte achter groepsimmuniteit. Nu weet je ook waarom het belangrijk is.
Mocht U meer willen weten over binomiale verdeling, koekeloert dan hier: https://www.dr-aart.nl/Kans-binomiale-verdeling.html
Met dank aan Rossella Bargiacchi
